V международный конкурс научно-исследовательских и творческих работ учащихся старт в науке

Расчет площади земельного участка

Наиболее точно рассчитать площадь участка земли можно аналитическим методом. Точность такого метода определена тем, что на него влияют только ошибки полевых измерений. Для участков простой формы используются простые формулы геометрии.

Для участков с более сложной формой расчеты производятся по координатам поворотных точек, а для сверх сложных участков используются программы, исходными данными для которых являются углы азимута точек.

Определение площади

Существует несколько способов такого определения площади участков земли:

Если вы хотите узнать, как в 2019 году решить именно Вашу проблему, обращайтесь через форму онлайн-консультанта или звоните по телефонам:

• Москва: +7 (499) 110-86-72.
• Санкт-Петербург: +7 (812) 245-61-57.

• аналитический;
• графический;
• механический.

Наиболее точным из этих методов является аналитический. Это связано с тем, что при его использовании на точность результатов влияют только ошибки полевых измерений, тогда как на два других метода оказывают влияние ошибки плана или карты, с которых снимаются данные.

Расчет площади аналитическим методом

При использовании аналитического способа площадь определяется по данным полевых измерений или по координатам поворотных точек, являющихся функциями результатов полевых измерений.

Участки имеют разные геометрические формы. В частности, они могут иметь четырехугольную форму.

Такая форма участка часто существует в старых садоводческих товариществах, в которых нарезались участки в 6 соток.

Если участок имеет форму трапеции и известны основные параметры такой фигуры, то площадь участка может быть рассчитана по формуле:

Если вы хотите узнать, как решить именно Вашу проблему, обращайтесь через форму онлайн-консультанта или звоните по телефонам:

• Москва: +7 (499) 110-86-72.
• Санкт-Петербург: +7 (812) 245-61-57.

• a и b – основания фигуры;
• h – высота трапеции.

Если известны координаты поворотных точек , то площадь надела может быть определена по приведенной ниже общей формуле для многоугольника. При этом для трапеции расчет площади производится по формуле с учетом того, что n=4.

При расчете четырехугольника неправильной формы, когда известны величины каждой из его сторон, необходимо определить величину периметра 2p:

2р=(а+b+c+d), где:

a,b,c,d – величины сторон.

Тогда площадь участка Sнф будет равна:

Sнф=√(p-a)(p-b)(p-c)(p-d).

В формуле используется значение половины периметра p.

Если участок имеет форму многоугольника с n сторонами, то его площадь рассчитывается по координатам поворотных точек:

Sу= 0,5*∑(Xi*(Yi+1-Yi-1), где:

• Xi и Yi – координаты i-той поворотной точки участка, имеющего вид многоугольника;
• i – порядковый номер точки. Этот параметр меняется от 1 до n;
• n – число характерных точек.

Для проверки правильности расчетов используется другая формула:

Sу1= 0,5*∑(Yi*(Xi+1-Xi-1).

Если расчеты проведены правильно, то Sу1 = Sу.

При наличии участка сложной формы со многими точками поворота расчет по приведенным выше формулам может стать затруднительным.

В этом случае аналитический расчет площади участка производится с использованием данных об углах азимута.

При этом по контуру границ участка производится замер азимута каждой поворотной точки. Также определяется расстояние от одной точки до следующей за ней точки.

Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади земельного надела.

Точность расчетов площади

При определении площади участка необходимо учитывать погрешности расчета площади.

В частности, если площадь участка рассчитана по координатам поворотных точек, то разница между расчетным и зафиксированным в ЕГРН значениями площади ЗУ не должна быть больше допустимой величины (dSдоп).

В нормативных документах эта величина определена следующим образом:

dSдоп=3,5*Mt*√Sу где:

• Mt – погрешность (СКП) расположения поворотной точки;
• Sy-площадь участка.

При этом если dS превышает допустимую величину, то необходимо провести проверку точности координат и методики расчета площади участка.

Если же dS оказывается меньше допустимого значения, то за окончательное значение площади может быть принято расчетное значение площади с указанием допустимого значения dPдоп.

Пример.

Вычисленная площадь участка № 103 снт “Изобретатель” составила 594 кв. м. По документам площадь участка равна 600 кв. м.

СКП Мt при межевании для садоводческих товариществ определена нормативно (приказ МЭР №518) и равна 20 см. Тогда:

dS = 600-594= 6 кв. м

dSдоп=3,5*0,2* √600=17,14 кв. м

Окончательное значение площади участка №103 Sy=594±17 кв. м.

• Москва: +7 (499) 110-86-72.
• Санкт-Петербург: +7 (812) 245-61-57.

1.1.Масштабы карт

Масштаб карты показывает, во сколько раз длина линии на карте меньше соответствующей ей длины на местности. Он выражается в виде отношения двух чисел. Например, масштаб 1:50 000 означает, что все линии местности изображены на карте с уменьшением в 50000 раз, т. е. 1 см на карте соответствует 50000 см (или 500 м) на местности.

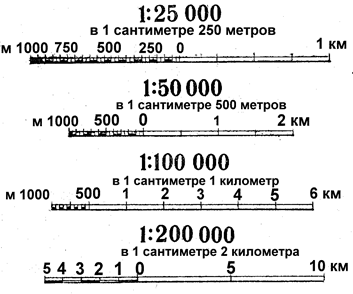Рис. 1. Оформление численного и линейного масштабов на топографических картах и планах городов

Масштаб указывается под нижней стороной рамки карты в цифровом выражении (численный масштаб) и в виде прямой линии (линейный масштаб), на отрезках которой подписаны соответствующие им расстояния на местности (рис. 1). Здесь же указывается и величина масштаба — расстояние в метрах (или километрах) на местности, соответствующее одному сантиметру на карте.

Полезно запомнить правило: если в правой части отношения зачеркнуть два последних нуля, то оставшееся число покажет, сколько метров на местности соответствует 1 см на карте, т. е. величину масштаба.

При сравнении нескольких масштабов более крупным будет тот, у которого число в правой части отношения меньше. Допустим, что на один и тот же участок местности имеются карты масштабов 1:25000, 1:50000 и 1:100000. Из них масштаб 1:25000 будет самым крупным, а масштаб 1:100 000-самым мелким.
Чем крупнее масштаб карты, тем подробнее на ней изображена местность. С уменьшением масштаба карты уменьшается и количество наносимых на нее деталей местности

Подробность изображения местности на топографических картах зависит от ее характера: чем меньше деталей содержит местность, тем полнее они отображаются на картах более мелких масштабов.

В нашей стране и многих других странах в качестве основных масштабов топографических карт приняты: 1:10000, 1:25000, 1: 50000, 1: 100000, 1: 200000, 1: 500000 и 1:1000000.

Используемые в войсках карты подразделяются на крупномасштабные, среднемасштабные и мелкомасштабные.

Масштаб карты	Наименование карты	Классификация карт
по масштабам	по основному назначению
1:10 000 (в 1 см 100 м)	десятитысячная	крупномасштабные	тактические
1:25 000 (в 1 см 250 м)	двадцатипятитысячная
1:50 000 (в 1 см 500 м)	пятитысячная
1:100 000 ( в 1 см 1 км)	стотысячная	среднемасштабные
1:200 000 (в 1 см 2 км)	двухсоттысячная	оперативные
1:500 000 (в 1 см 5 км)	пятисоттысячная	мелкомасштабные
1:1 000 000 ( в 1 см 10 км)	миллионная

Азимуты и дирекционный угол. Магнитное склонение, сближение меридианов и поправка направления

Истинный азимут (Аи) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением истинного меридиана данной точки и направлением на объект (см. рис. 7).

Магнитный азимут (Ам) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0е до 360° между северным направлением магнитного меридиана данной точки и направлением на объект.

Дирекционный угол (α; ДУ) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением вертикальной линии координатной сетки данной точки и направлением на объект.

Магнитное склонение (δ; Ск) — угол между северным направлением истинного и магнитного меридианов в данной точке.

Если магнитная стрелка отклоняется от истинного меридиана к востоку, то склонение восточное (учитывается со знаком +), при отклонении магнитной стрелки к западу — западное (учитывается со знаком -).

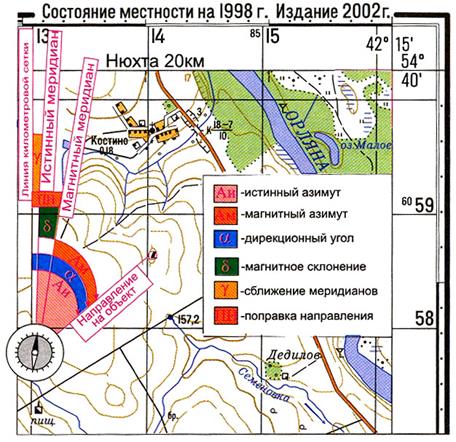Рис. 7. Углы, направления и их взаимосвязь на карте

Сближение меридианов (γ; Сб) — угол между северным направлением истинного меридиана и вертикальной линией координатной сетки в данной точке. При отклонении линии сетки к востоку – сближение меридиана восточное (учитывается со знаком +), при отклонении линии сетки к западу — западное (учитывается со знаком -).

Поправка направления (ПН) — угол между северным направлением вертикальной линии координатной сетки и направлением магнитного меридиана. Она равна алгебраической разности магнитного склонения и сближения меридианов:

Площадь фигуры, её свойства. Способы измерения площадей фигур. Единицы площади. Вычисление площадей квадрата, прямоугольника, треугольника, круга, трапеции.

Первое представление о площадях – в дошк. возрасте (н-р: сравнивая платочки).Геометр фигура плоская, если все точки принадлежат 1 плоскости. S фигуры – положит величина, определяется для каждой фигуры, так что: 1) равные фигуры имеют = S; 2) S фигуры = сумме S всех ее компонентов. Равные фигуры – совпадают при наложении. Равновеликие – S равны. Равносоставленные – две фигуры, которые можно разбить на соответ равные части (только многоугольники). Теорема Бойян и Гервина: 1) равносоставленные фигуры = равновеликие; 2) если у 2 многоугольников S =, то их можно представить из 2 попрано = частей.

Св-ва S: 1)если фигуры =, то = их числ значения S; 2) если фигура состоит из частей, то S = сумме S этих частей; 3) при замене ед S, числ значение S увеличивается во столько раз, во сколько ед S; 4) числ значение S единичного квадрата = 1; 5) если F₁ – часть F₂, то численное значение F₁ 2 2 . Чтобы найти приближенное значение S_(F) достаточно сложить получ числовые значения S по недостатку и по избытку :2. S_(F)

(me+(m+n)e 2 )/2 = ((m+n+m)e 2 )/2= (2m/2 +n/2)e 2 = (m+n/2)e 2 . Для более точно значения – более мелкая палетка, или наклонить с разных углов, и высчитать среднее арифметическое.

Ед S. м 2 , см 2 , дм 2 , км 2 , мм 2 , ар, га, сотка.

Формулы площади квадрата

1) Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны. S = a2

2) Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — Площадь квадрата, a — длина стороны квадрата, d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b, где S — Площадь прямоугольника, a, b — длины сторон прямоугольника.

Формулы площади треугольника

1) Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты. S = 1 a · h

2) Формула площади треугольника по трем сторонам

Формула Герона: S = √p(p — a)(p — b)(p — c)

3) Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. S = 1 a · b · sin γ

4) Формула площади треугольника по трем сторонам и радиусу описанной окружности.

5) Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. S = p · r, где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности,

p = a + b + c — полупериметр треугольника.

Формулы площади круга

1) Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи. S = π r2

2) Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи. S = 1 π d2

где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга.

Формулы площади трапеции

1) Формула Герона для трапеции

S = a + b √(p — a)(p — b)(p — a — c)(p — a — d)

2) Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

где S — площадь трапеции,a, b — длины основ трапеции, c, d — длины боковых сторон трапеции, p = a + b + c + d — полупериметр трапеции.

Источник

Как определить границы участка по кадастровому номеру

Рассмотрите с помощью программы ФИР ГКН два участка, которые имеют установленные границы, чтобы можно было отобразить эти участки на карте для определения границ. Для этого необходимо скачать оба электронных документа в формате .xml, которые отражают данные земельных участков.

Скачанные документы будут представлены в виде архива файлов. Чтобы удобнее было работать с ними, необходимо распаковать их. После распаковки документов их можно будет открыть с помощью программы геокалькулятора Росреестра.

Далее необходимо в программе геокалькулятора установить систему координат. Для этого необходимо посмотреть в кадастровом документе, какая обозначена система координат. Для этого откройте выписку и найдите строку № 14.

Далее, в левой части всплывающего окна установите исходную систему координат, которая обозначена в кадастре. При этом если в системах координат после нажатия кнопки меню для синхронизации координат не найдена требуемая система координат, воспользуйтесь файлом проекции, в который внесены параметры системы координат.

Для этого необходимо открыть файл проекции, созданный в формате prj, который расположен в корневой папке с установочным файлом программы геокалькулятор.

После загрузки существующих систем координат из указанного файла выберите необходимую в данном случае систему координат. При выборе необходимой системы из списка необходимо будет присвоить название этой системе координат. Чаще всего в качестве названия применяется официальное наименование системы координат, чтобы не путаться.

Затем, в левой части программы геокалькулятора выбираете требуемую систему координат, далее, обязательно выбираете в графе «Датум» элемент Pulkovo 1942(ГОСТ). Затем подтверждаете настройки нажатием кнопки «Выбрать».

Указанные выше параметры применяются для точного позиционирования участка земли на местности. При таких настройках ошибка в координатах сводится к минимальным показателям допустимой погрешности.

Далее, в левой части окна выбираете систему координат со следующими настройками:

• В графе «Группа» устанавливаете параметр общеземной системы координат «Широта\долгота»;
• Система – WGS84 (Широта\Долгота);
• Калибровка – этот параметр не меняется;
• Датум – WGS84.

Далее, выбираете в правом окне в графе конвертирования файлов в указанный формат файл с расширением .gpx.

Затем установите галочки напротив следующих опций:

• Создавать точки;
• Создавать имена участников, как точки;
• Создавать треки.

Другие опции не включать.

После выставления необходимых параметров в окнах предварительной настройки слева внизу нажмите на кнопку для начала процесса конвертации. В результате указанных действий справа в окне с информацией будут отображены 2 файла, переведенные в формат треков. Такие файлы могут быть открыты в различных программах, однако, открывайте их в программе «SAS. Планета».

Плюс этой программы в удобстве использования информации и наглядности, кроме этого, программа общедоступна и бесплатна для применения.

Границы участка по кадастровому номеру со спутника.

Об уточнении местоположения границ земельного участка, поставленного на кадастровый учет, читайте тут.

Для этого открывайте файлы треков путем запуска их через указанную программу. В открытом окне с параметрами импорта файлов в строке «Категория» укажите кадастровый номер участка земли. После внесения данных о номере кадастрового регистрационного учета нажмите «Начать», затем, всплывающее окно информации закрывайте нажатием на кнопку «Yes».

В результате совершения правильных действий на экране будут видны координаты границ участков земли, которые изображены в виде красных линий с указанными контрольными точками.

Имейте в виду: при конвертации контрольных точек можно выбрать свойства каждой точки и посмотреть координаты долготы и широты, если выбрана система координат с названием «Географические». Такие данные удобно применять для обнаружения объекта с помощью навигаторов различных типов.

Измерение и построение дирекционных углов на карте. Переход от дирекционного угла к магнитному азимуту и обратно

На местности при помощи компаса (буссоли) измеряют магнитные азимуты направлений, от которых затем переходят к дирекционным углам.

На карте наоборот, измеряют дирекционные углы и от них переходят к магнитным азимутам направлений на местности.

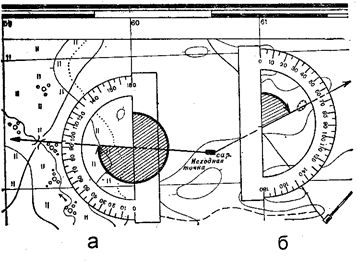Рис. 8. Изменение дирекционных угловна карте транспортиром

Дирекционные углы на карте измеряются транспортиром или хордоугломером.

Измерение дирекционных углов транспортиром производят в следующей последовательности:

• ориентир, на который измеряют дирекционный угол, соединяют прямой линией с точкой стояния так, чтобы эта прямая была больше радиуса транспортира и пересекала хотя бы одну вертикальную линию координатной сетки;
• совмещают центр транспортира с точкой пересечения, как показано на рис. 8 и отсчитывают по транспортиру значение дирекционного угла. В нашем примере дирекционный угол с точкой А на точку В равен 274° (рис. 8, а), а с точки А на точку С – 65° (рис. 8, б).

На практике часто возникает необходимость в определении магнитного АМ по известному дирекционному углу ά , или, наоборот, угла ά no известному магнитному азимуту.

Переход от дирекционного угла к магнитному азимуту и обратно

Переход от дирекционного угла к магнитному азимуту и обратно выполняют тогда, когда на местности необходимо с помощью компаса (буссоли) найти направление, дирекционный угол которого измерен по карте, или наоборот, когда на карту необходимо нанести направление, магнитный азимут которого измерен, на местности с помощью компаса.

Для решения этой задачи необходимо знать величину отклонения магнитного меридиана данной точки от вертикальной километровой линии. Эту величину называют поправкой направления (ПН).

Рис. 9. Схема магнитного склонения, сближения меридианов и поправка направления

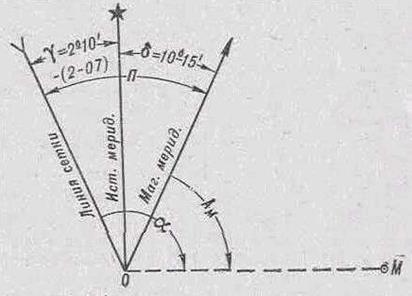Рис. 10. Определение поправки для перехода от дирекционного угла к магнитному азимуту и обратно

Поправка направления и составляющие ее углы — сближение меридианов и магнитное склонение указываются на карте под южной стороной рамки в виде схемы, имеющей вид, показанный на рис. 9.

Сближение меридианов (g) — угол между истинным меридианом точки и вертикальной километровой линией зависит от удаления этой точки от осевого меридиана зоны и может иметь значение от 0 до ±3°. На схеме показывают среднее для данного листа карты сближение меридианов.

Магнитное склонение (d) — угол между истинным и магнитным меридианами указан на схеме на год съемки (обновления) карты. В тексте, помещаемом рядом со схемой, приводятся сведения о направлении и величине годового изменения магнитного склонения.

Чтобы избежать ошибок в определении величины и знака поправки направления, рекомендуется следующий прием.

Из вершины углов на схеме (рис. 10) провести произвольное направление ОМ и обозначить дужками дирекционный угол ά и магнитный азимут Ам этого направления. Тогда сразу будет видно, каковы величина и знак поправки направления.

Если, например, ά = 97°12′, то Ам = 97°12′ — (2°10’+10°15′) = 84°47‘.

Площадь фигуры, ее основные свойства. Способы измерения площадей фигур. Единицы площади

1. Площадь фигуры.

2. Способы измерения площади фигуры.

3. Равновеликие и равносоставленные фигуры.

4. Единицы площади. Отношения между ними.

5. Измерение площадей простейших фигур.

6. Измерение площадей фигур в начальной школе.

Рассмотрим вопрос о площади плоской фигуры и способах измерения площадей.

Дадим аксиоматическое определение площади, согласно и аксиоматическим определениям темы 1.

Функцией площади называется любая функция S : U R_>0, обладающая свойствами:

1) конечной аддитивности, т.е. » u, v Є u,

2) Gs — инвариантности, т.е. «u Є U, » g Є (L₂ х R 2 ),

Рассмотрим основы теории измерения площадей плоских фигур, взяв за основу подход, впервые изложенный французским математиком К. Жорданом согласно.

Пусть М — множество фигур на плоскости, имеющих замкнутых контур, и Ф — одна из таких фигур, площадь которой надо измерить. По отношению к фигуре Ф будем различать внутренние и внешние точки, а так же точки контура. Далее, через производную точку плоскости проведем две взаимно перпендикулярные прямые (оси) и выберем единичный отрезок l. Откладывая на каждой прямой единичный отрезки, равные единичному, и проведя через их концы прямые, параллельные осям, получим на плоскости сеть квадратов (рис. 1), площадь каждого из которых равна единице.

Заштрихуем те квадраты, через которые проходит контур фигуры Ф. Тогда по отношению к фигуре Ф выделяются квадраты трех видов:

1) квадраты, целиком состоящие из внутренних точек фигуры Ф;

2) квадраты, состоящие как из внутренних, так и внешних точек фигуры (на рис. 1 они заштрихованы);

3) квадраты, не содержащие внутренних точек фигуры Ф.

покрывающей

Система квадратов, состоящая из всех квадратов первого вида, называется внутренней системой квадратов по отношению к фигуре Ф.

Численные значения площадей внутренней и покрывающей систем квадратов легко подсчитать. Если рассматривать только единичные квадраты, то эти значения выражаются натуральными числами m₁ и n₁ соответственно. Здесь m₁ — число единичных квадратов, целиком лежащих внутри фигуры Ф, а n₁ — число единичных квадратов покрывающей системы для фигуры Ф. Таким образом, m₁ и n₁ будут приближенными значениями измеряемой площади: первое m₁ — с недостатком; второе n₁ — с избытком.

Разделим каждую из сторон единичного квадрата на 10 равных частей и проведем через точки деления прямые, параллельные сторонам квадрата. При этом единичный квадрат разложится на 100 равных квадратов. Пользуясь новым квадратом, образуем на плоскости более мелкую сеть. Обозначим через m₂ и n₂ число новых квадратов внутренней и покрывающей систем, соответственно. Тогда числа

Деля каждую из сторон малых квадратов снова на 10 равных частей, образуем еще более мелкую сеть. При этом числа

Кроме того, для любого j > 1 имеем:

Из соотношения

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Круг — это когда множество точек на плоскости удалены от центра на равном радиусу расстоянии. Радиусом принято называть прямую линию, соединяющую центр с любой точкой окружности.

1. S = π * r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

2. S = d 2 : 4 * π, где d — это диаметр.

3. S = L 2 ​ : 4 * π, где L — это длина окружности.

Как без труда рассчитать площадь участка сложного контура

Большинство зарегистрированных земельных участков (ЗУ) имеют установленные границы, которые определяются межевыми знаками, природными урочищами и искусственными объектами.

Проводить межевание земельных наделов необходимо, чтобы отделить участок от соседних ЗУ, общественных территорий, а также зон сервитута. По границам можно определить контур участка и рассчитать его площадь.

Площадь является важной характеристикой земельного участка:

• по ней устанавливается его кадастровая или рыночная стоимость;
• производится планировка;
• устанавливается земельный налог.

Если контур ЗУ представляет собой правильный прямоугольник, то рассчитать его площадь не представляет сложности: для этого достаточно длину стороны, А умножить на длину стороны В. Но гораздо чаще очертания ЗУ имеют неправильную форму, и тогда для расчета лучше использовать калькулятор площади земельного участка.

Калькулятор площади земельного участка

Этот калькулятор крайне прост в использовании — нужно просто измерить стороны А, В, С и D и вставить значения в калькулятор.

Если ЗУ имеет правильную прямоугольную форму, сторона, А принимается равной D, а B — С. Например, чтобы рассчитать площадь земельного надела длиной 103 м, шириной 57 м, нужно заполнить поля в следующей последовательности: А — 103 м, В — 57 м, С — 57 м, D — 103 м.

Расчет площади участка сложного контура

Если контур земельного участка — это сложная фигура, то ее можно разбить на две и более фигур.

Например, пятиугольник на рисунке ниже состоит из треугольника EFC и четырехугольника ABCD. Площадь четырехугольника S рассчитывается уже известным нам способом. Что касается площади треугольника, то она равна половине площади четырехугольника EHFJ, в том случае если один из углов треугольника равен 90 градусов (прямоугольный треугольник).

Зададим длины сторон сложного контура ЗУ: А = 80 м; В = 70 м; С = 75 м; D = 60 м; E = 60 м; F = 50 м.

• Вначале рассчитаем площадь фигуры ABCD, подставив в калькулятор значения сторон А, В, С и D: Sabcd = 5023 м2.
• Теперь определим S фигуры EHFJ, подставив в качестве, А и D — Е (60), В и С — F (50): Sehfi = 3000 м2.
• Площадь треугольника EFC: Sefc = 3000/2 = 1500 м2.
• S земельного участка: 5023 + 1500 = 6023 м2.

Однако если треугольник не прямоугольный, расчет Sefc следует производить по другим формулам, в частности, как половину произведения высоты треугольника h на его основание C.

Например, если h равна 45 м, а С — 75 м, то Sefc будет равна ½×45×75 = 1687 м2.

Sзу = 5023 + 1687 = 6710 м2.

Практическое применение калькулятора

Знание площади ЗУ позволяет определить величину земельного налога. Например, известны:

• средняя кадастровая стоимость одного метра земли в регионе — 5000 руб/м2;
• размеры участка А, В, С и D — 40, 30, 35 и 20 м2 соответственно;
• расположение надела в жилой зоне, то есть ставка налогообложения — 1,5%.

Площадь, рассчитанная по калькулятору площади ЗУ — 924,47 м2 или 9,24 сотки.

Дальнейший расчет:

• Кадастровая стоимость: КС = 5000×924,47 = 4 622 350 руб.
• Величина земельного налога ЗН = 1,5% х 4 622 350 = 69 335 руб.

Эту сумму необходимо будет выплачивать ежегодно.

Использовать калькулятор следует для ориентировочной оценки стоимости земельного надела и имущественного налога, если участок новый и еще не поставлен на кадастровый учет. Если ЗУ зарегистрирован в ЕГРН, узнать его точную стоимость и площадь можно на сайте Росреестра, введя в поле поисковой формы кадастровый номер или адрес участка.

Другой вариант — воспользоваться земельным калькулятором в виде карты, который даст результат только в том случае, если ЗУ есть в базе данных.

От чего зависит кадастровая стоимость и налог

Величина кадастровой стоимости земли зависит от многих факторов:

• региона;
• географического положения участка;
• назначения земли и т. д.

Земельные наделы в землях под ведение фермерского хозяйства, ЛПХ, сельскохозяйственной деятельности могут быть намного дешевле ЗУ под ИЖС.

На величину налога оказывают влияние:

• налоговая ставка, которая может быть разной в различных регионах;
• наличие льгот (все категории льготников перечислены в ст. 391 НК РФ).

Межевание земли

Чтобы определить точные границы участка, необходимо провести межевание, которое отделит земельный надел от соседних частных участков и территории публичного пользования.

• Надо вызвать кадастрового специалиста, который проведет геодезические съемки, привяжет данный надел к единым государственным координатам, а в точках поворотах контура установит межевые знаки.
• После того как межи установлены, можно смело приступать к замеру длин сторон и расчету площади, а также планировке строительных работ.

Калькулятор площади земельного участка

Загрузка…

Площадь фигуры, ее основные свойства. Способы измерения площадей фигур. Единицы площади

1. Площадь фигуры.

2. Способы измерения площади фигуры.

3. Равновеликие и равносоставленные фигуры.

4. Единицы площади. Отношения между ними.

5. Измерение площадей простейших фигур.

6. Измерение площадей фигур в начальной школе.

Рассмотрим вопрос о площади плоской фигуры и способах измерения площадей.

Дадим аксиоматическое определение площади, согласно и аксиоматическим определениям темы 1.

Функцией площади называется любая функция S : U R_>0, обладающая свойствами:

1) конечной аддитивности, т.е. » u, v Є u,

2) Gs — инвариантности, т.е. «u Є U, » g Є (L₂ х R 2 ),

Рассмотрим основы теории измерения площадей плоских фигур, взяв за основу подход, впервые изложенный французским математиком К. Жорданом согласно.

Пусть М — множество фигур на плоскости, имеющих замкнутых контур, и Ф — одна из таких фигур, площадь которой надо измерить. По отношению к фигуре Ф будем различать внутренние и внешние точки, а так же точки контура. Далее, через производную точку плоскости проведем две взаимно перпендикулярные прямые (оси) и выберем единичный отрезок l. Откладывая на каждой прямой единичный отрезки, равные единичному, и проведя через их концы прямые, параллельные осям, получим на плоскости сеть квадратов (рис. 1), площадь каждого из которых равна единице.

Заштрихуем те квадраты, через которые проходит контур фигуры Ф. Тогда по отношению к фигуре Ф выделяются квадраты трех видов:

1) квадраты, целиком состоящие из внутренних точек фигуры Ф;

2) квадраты, состоящие как из внутренних, так и внешних точек фигуры (на рис. 1 они заштрихованы);

3) квадраты, не содержащие внутренних точек фигуры Ф.

покрывающей

Система квадратов, состоящая из всех квадратов первого вида, называется внутренней системой квадратов по отношению к фигуре Ф.

Численные значения площадей внутренней и покрывающей систем квадратов легко подсчитать. Если рассматривать только единичные квадраты, то эти значения выражаются натуральными числами m₁ и n₁ соответственно. Здесь m₁ — число единичных квадратов, целиком лежащих внутри фигуры Ф, а n₁ — число единичных квадратов покрывающей системы для фигуры Ф. Таким образом, m₁ и n₁ будут приближенными значениями измеряемой площади: первое m₁ — с недостатком; второе n₁ — с избытком.

Разделим каждую из сторон единичного квадрата на 10 равных частей и проведем через точки деления прямые, параллельные сторонам квадрата. При этом единичный квадрат разложится на 100 равных квадратов. Пользуясь новым квадратом, образуем на плоскости более мелкую сеть. Обозначим через m₂ и n₂ число новых квадратов внутренней и покрывающей систем, соответственно. Тогда числа

Деля каждую из сторон малых квадратов снова на 10 равных частей, образуем еще более мелкую сеть. При этом числа

Кроме того, для любого j > 1 имеем:

Из соотношения

Число s называют значением внутренней площади фигуры Ф, а число S — значением внешней площади. Очевидно, что s £ S, т.к. при любом номере i имеет место неравенство m_i £ n_i.

4.1. Способы определения площадей

Площади угодий на землеустроительном плане можно определить аналитическим, графическим и механическими способами

Самый точный способ вычисления площадей основан на использовании координат вершин участка, определяемых по результатам полевых измерений и математической обработки длин линий и углов между ними (аналитический способ).

Вычисление площади участка по координатам производится по формулам:

т.е. удвоенная площадь землепользования равна сумме произведений каждой абсциссы на разность ординат последующей и предыдущей точек.

Результаты вычислений по этим формулам взаимно контролируются. В процессе вычислений разности контролируются тем, что суммы их равны нулю.

Таблица 6

Вычисление площади землепользования по координатам

Алгебраические суммы чисел в 4-й и 6-й графах должны быть равны нулю, а в 5-й и 7-й – равны между собой. Эти равные суммы выражают удвоенную сумму площади землепользования.

При вычислении площади графическим способом (см.: Маслов А.В., Юнусов А.Г., Горохов Г.И. Геодезические работы при землеустройстве: Учебное пособие для вузов. М.: Недра, 1990. – 215 с., п.29, С.65) участки изображенные на плане, разбивают на простейшие геометрические фигуры (треугольники, трапеции, прямоугольники, квадраты). Чем больше углов имеет граница землепользования, тем меньше точность вычисления площадей отдельных фигур, а значит и всего землепользования.

Площадь землепользования, вычисленную графически сравнивают с аналитической, она не должна отличаться от аналитической на величину допустимой невязки:

,                       (8)

где f – допустимая невязка;

Р_ан – площадь участка землепользования по координатам (аналитический способ);

М – масштаб.

,                                    (9)

где Р_треуг – площадь участка землепользования, подсчитанная по треугольникам (графический способ).

Элементы, измеряемые в простейших фигурах для вычисления их площадей, показаны на рисунке 13.

Измерив в масштабе плана величины, необходимые для определения площади – основание, высоту, параллельные стороны, определяют площадь каждой геометрической фигуры и затем берут их сумму.

1. Для треугольника (рис. 13,а)

,           (10)

где а, b, с – длины сторон;

h – высота;

c – угол между сторонами а и b треугольника;

р – полупериметр, р=1/2 (а+b+с);

2. Для параллелограмма (рис. 13,б)

           Р=аh                 (11)

3. Для трапеции (рис. 13,в)

           (12)

Рис.13. Элементы, измеряемые в простейших фигурах  для вычисления их площади

4. Для четырехугольника (рис. 13,г)

,           (13)

где L и К – диагонали;

 – угол между диагоналями.

Чтобы проконтролировать результаты определения площади, необходимо повторить вычисления, меняя исходные данные. Все вычисления вести как показано в таблице 7, занося туда длины линий, определяемые по плану.

Рис. 14. Разбивка полигона на фигуры при определении площади графическим способом

Например, в треугольнике (рис. 14) можно измерить две высоты h₁=145м и h₂=168 м и две стороны на которые они опущены а₁=540 м и а₂=465 м.

Таблица 7

№ треугольника	Основание, м	Высота, м	Половина произведений	Средняя площадь, м2
1	540 465	145 168	39150 39060	39105

Предыдущая