Как высчитать квадратные метры комнаты: расчет площади нестандартных помещений

Как рассчитать площадь окон чтобы дом не был темным

При проектировании и строительстве жилого дома нужно руководствоваться содержанием СанПиН 2.1.2.2645-10. Согласно этому нормативному акту все помещения жилого назначения обязаны иметь световые проемы в наружных стенах здания. Количество окон жилых комнат и кухни должно быть таким, чтобы коэффициент естественного освещения был не ниже 0,5. Нормы инсоляции установлены нормативной документацией с учетом:

• географической широты расположения объекта;
• календарного периода;
• функционала помещения;
• планировочной зоны города.

Хотя бы одна из комнат 1-3 комнатной квартиры должна иметь уровень освещенности, соответствующий установленным нормативам. Когда же квартира состоит из более чем 4-х комнат, то удовлетворительное освещение должно быть в 2-х и более комнатах.

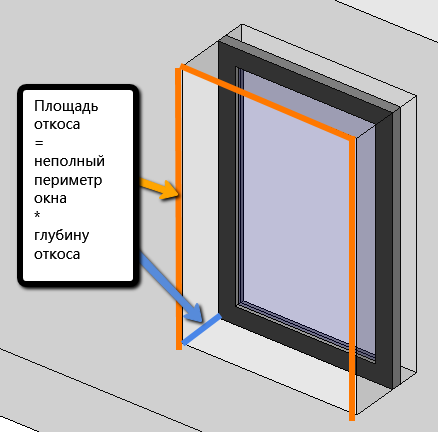
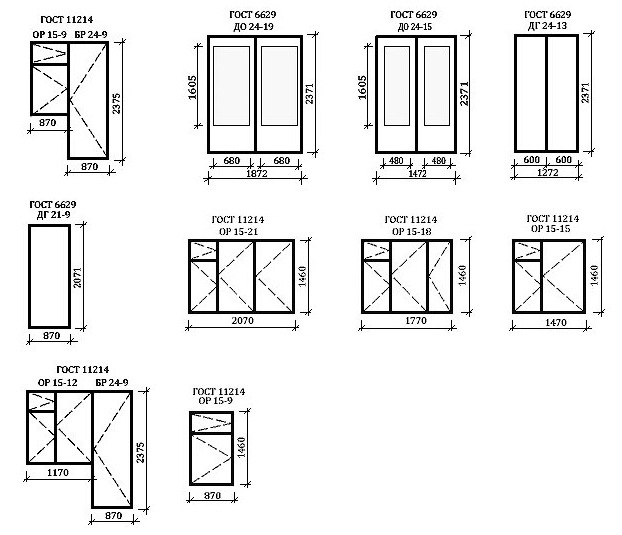
Исходя из строительных правил, можно рассчитать квадратуру окон для каждого помещения в жилом доме:

1. Замерить площадь пола каждого отдельно взятого помещения.
2. Определить минимально допустимую площадь остекления, посчитав 10 – 12,5% от полученной площади пола комнаты.

При проектировании световых архитектурных элементов нужно учитывать, что итоговый метраж остекления будет меньше оставленного проема. Это объясняется наличием у любого окна светонепроницаемой коробки, используемой для монтажа окна и крепления стекол внутри оконного блока.

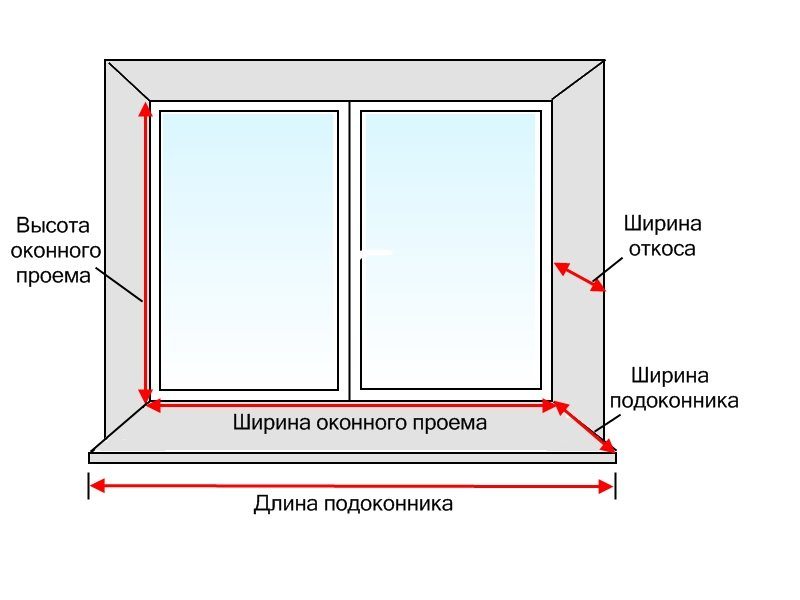
Принято считать, что наиболее комфортной для самочувствия человека является суммарная ширина окон помещения, составляющая от 55% ширины комнаты. Если оконный проем единственный, то его нужно расположить по центру самой длинной наружной стены.

Уровень инсоляции можно регулировать размещением конструктивного элемента по вертикали: чем выше проем относительно пола, тем больше освещенность. Это условие справедливо в том случае, когда в непосредственной близости нет высоких зданий или деревьев, затрудняющих проникновение солнечных лучей.

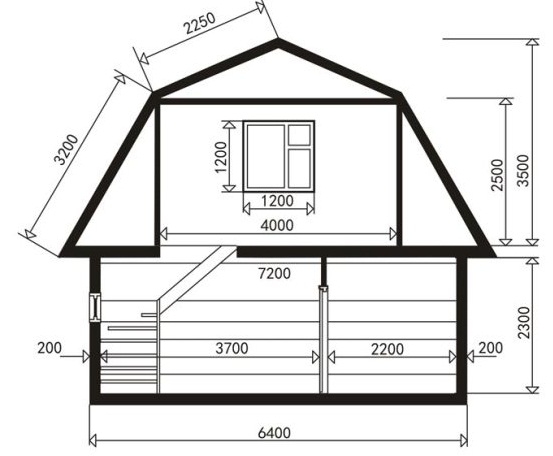
На этапе проектирования при расчете поверхности остекления необходимо ориентироваться на правила по тепловой защите зданий. Согласно этим правилам коэффициент остекленности фасада в жилом доме не превышает 18% с учетом сопротивления теплопередачи световых и вентиляционных отверстий.

Допустима установка в частных жилых домах зенитных фонарей, представляющих собой окна сложной и нестандартной геометрической формы. Площадь таких световых проемов не должна превышать 15% от площади пола. В том случае, когда зенитный фонарь монтируется в мансардном помещении, площадь остекления может быть максимально равной 10% площади комнаты.

Площадь квадрата

Из известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– ) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это . Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I2<S (случай, когда I2>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его , для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Как рассчитать основные размеры окна

При проектировании жилья определяется минимальная площадь окон и место их установки. Исходя из этого, можно рассчитать более точные и конкретные параметры для каждого окна каждого помещения, чтобы узнать площадь остекления. При расчетах принято определять максимальную высоту окна для конкретного помещения, чтобы использовать оптимальные условия естественного освещения.

С учетом того, что высота подоконника – 70-90 см, а в домах с централизованным отоплением 80-90 см, а верхняя перемычка окна должна находиться не выше 15-25 см от потолка, легко просчитать максимальную высоту окна и применить к ней световое соотношение сторон – эти посчитанные параметры будут соответствовать требованиям СНиП.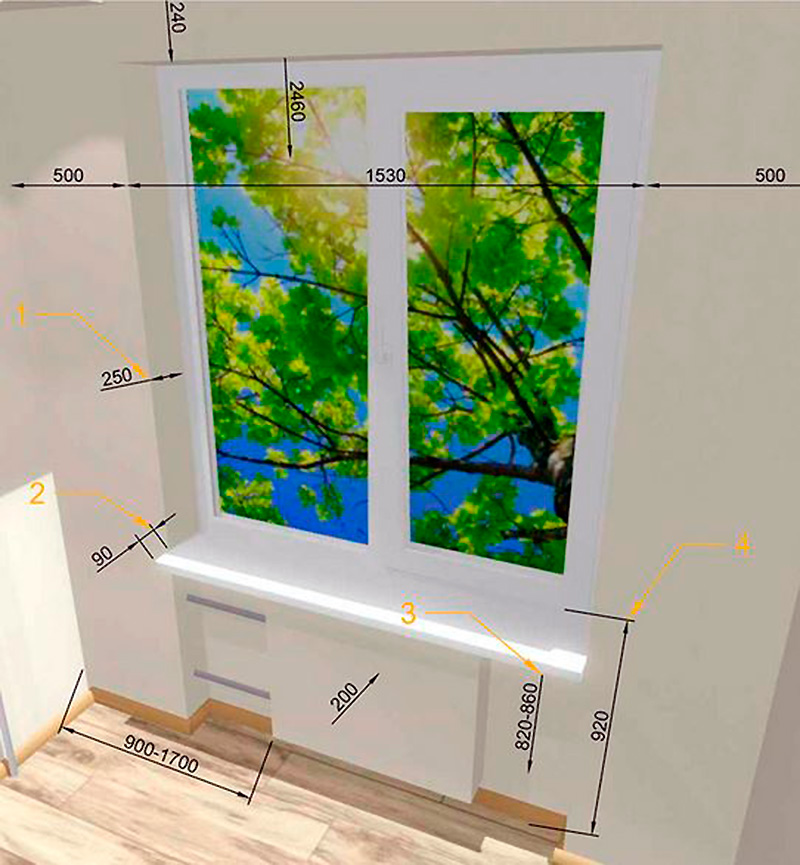

Согласно СНиП, при общей площади остекления, соответствующей 10-12% площади пола комнаты, в нее будет поступать минимальное количество естественного света. При этом оптимальной считается ширина оконного проема, соответствующая 55% от ширины комнаты.

Соотношение сторон окна играет больше визуальное значение, чем конструктивное. Также правильно выбранное соотношение сторон – это комфортность пользование фрамугами. Поэтому обычно за стандартные соотношения принимаются правильные пропорции, например, 8:13. Для расчета размеров окна существуют компьютерные программы, также можно прибегнуть и к помощи онлайн калькулятора.

Кроме того, существуют правила, которые необходимо соблюдать при проведении любых расчетов. Например, перед тем, как посчитать параметры окна и светового потока, принимается, что для одного жилого помещения угол падения естественного освещения через остекление должен быть 18-30 0 , а площадь остекления должна лежать в диапазоне 14-17% от общей площади пола в комнате.

При расчете параметров необходимо учитывать соседние строения – угол падения естественного потока света зависит от высоты расположения оконного проема и близости соседствующих с жильем зданий. Естественный поток освещения будет уменьшаться при уменьшении расстояния между домами, и наоборот. Это же относится и к углу падения освещенности – чем выше близлежащие строения, тем выше угол светового потока.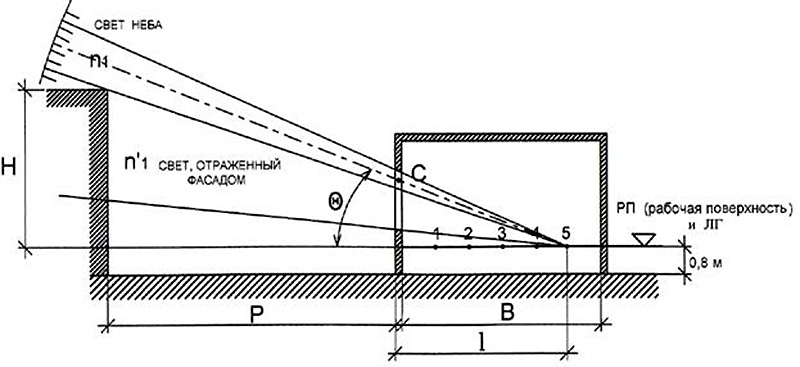

Окно в проектировании здания считается наиболее уязвимой поверхностью с точки зрения тепло- и энергообмена, поэтому любые стандартные расчеты требуют минимизации размеров окна, что приводит к уменьшению естественного светового потока через остекленную площадь. Чтобы не возникало конфликта между желанием увеличить освещение и тепловыми потерями, составлены и действуют соответствующие СНиП. По этим же рекомендациям, коэффициентам и формулам проектировщики проводят расчеты освещенности и естественных световых потоков для разных помещений.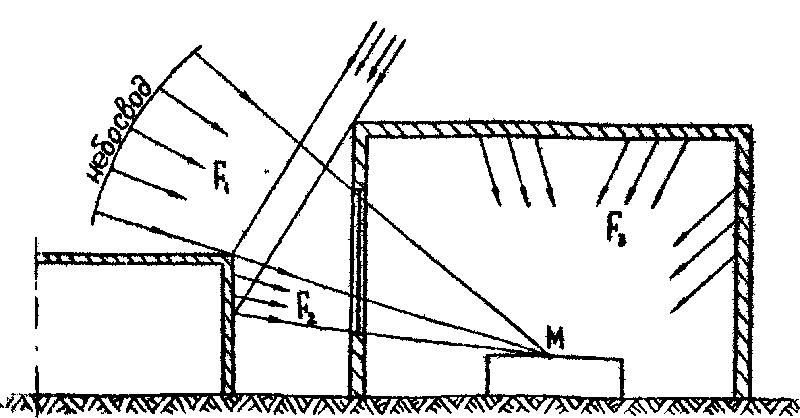

Результаты расчетов в виде соотношений сторон окна приведены ниже. Это примеры для объектов гражданского назначения, расположенных в средней полосе России на высоте ≤ 800 метров над уровнем моря, при незначительном затенении соседними объектами:

1. Помещения, предназначенные для проживания, включая номера в гостинице, ресторанные и торговые помещения: 1:8-1:6;
2. Помещения для приготовления пищи и коридоры: 1:10-1:8;
3. Лестничные марши и клетки: 1:14-1:10;
4. Учебные, детские и игровые помещения: 1:4-1:3;
5. Читальные и спортивные залы: 1:6-1:5;
6. Научные кабинеты и лаборатории: 1:7-1:5;
7. Помещения административного управления: 1:10-1:6;
8. Помещения медицинских кабинетов: 1:7-1:5;
9. Помещения для больных – палаты: 1:7-1:6;

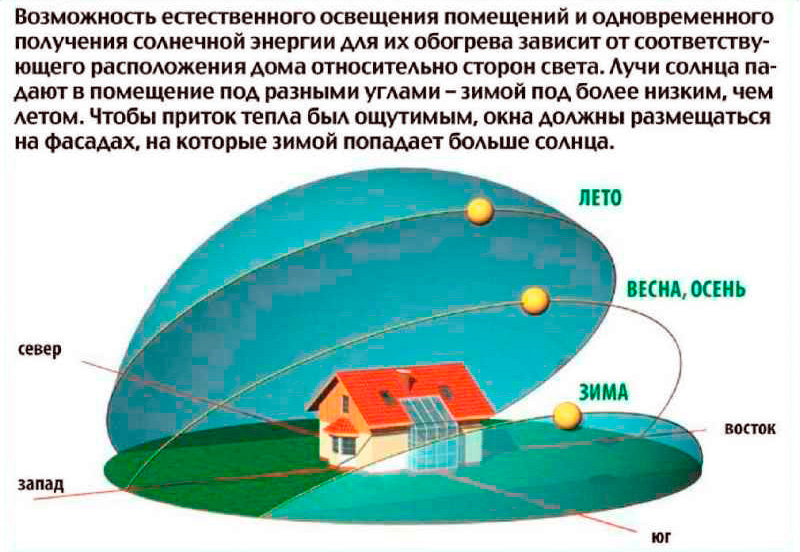
Но эти результаты площадей остекления и соотношения сторон проемов, рассчитанные по формулам, все же можно считать ориентировочными, так как отдельный расчет естественного освещения для каждого окна в помещении обязателен.

Формула площади прямоугольника

Для того, чтобы найти площадь прямоугольника без формулы необходимо посчитать количество единичных квадратов, на которые разбита фигура.

Рис. 1. Прямоугольник, разбитый на единичные квадраты

Прямоугольник разбит на 15 квадратов, то есть его площадь равна 15 см2

Стоит обратить внимание, что в ширину фигура занимает 3 квадрата, а в длину 5, поэтому чтобы вычислить количество единичных квадратов, необходимо умножить длину на ширину. Меньшая сторона четырехугольника – ширина, большая длина

Таким образом, можно вывести формулу площади прямоугольника:

S = a · b, где a,b – ширина и длина фигуры.

К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см2.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
2. Найдите квадрат известной стороны.
3. Отнимите от квадрата диаметра квадрат стороны.
4. Найдите квадратный корень разности.
5. Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

1. Квадрат диаметра: 10*10 = 100 см.
2. Квадрат стороны: 8*8 = 64 см.
3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
5. Умножаю сторону на корень из разности: 8*6 = 48 см.

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Что такое квадратный метр

Для начала надо определиться, что из себя представляет квадратный метр. Люди, которые плохо учили в школе математику, все равно рано или поздно сталкиваются с проблемой подсчета количества строительных материалов. Поэтому квадратный метр – основная точка отсчета при определении площади помещения.

Если нарисовать квадрат (это геометрическая фигура с одинаковыми сторонами), и сторона будет равна 100 см, то при умножении на 100 получим число 10000 см. это означает, что размер данной фигуры 10000 см2. Можно проще. Посчитать в метрах: 100 см – это 1 м. Применяем формулу подсчета площади – перемножаем две стороны, то есть 1 умножаем на 1, получаем 1 м. Значит, размер квадрата 1 кв.м.

Пространство неправильной формы

Как найти площадь комнаты, если она имеет нестандартную конфигурацию? Для начала разделите ее на несколько правильных геометрических фигур. Их можно нарисовать на простом листе бумаги. Затем определите площадь каждой из них, а результаты сложите. Как вычислять размеры классического пространства вам уже известно. Разберемся с остальным.

Круг

Как посчитать площадь комнаты, если она обладает круглой формой? Здесь вам также понадобятся общеизвестные геометрические формулы:

Трапеция

Рассматривая современные новостройки, можно заметить, что большинство из них имеет нестандартную трапециевидную форму. Но волноваться не стоит! Найти площадь такого пространства будет не сложнее, чем во всех предыдущих случаях.

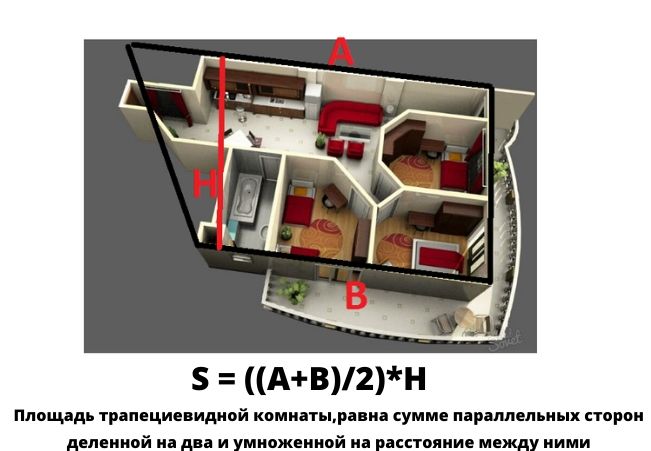
Выполнить измерения поможет простая формула

Комната с эркером

Посчитать квадратуру жилого пространства, дополненного нишами, эркерными окнами, выступами и другими сантехническими или интерьерными конструкциями, не составляет большого труда. Чтобы узнать общую площадь подобного помещения, разделите его на несколько отдельных участков и «поработайте» с каждым из них.

При этом нужно учитывать несколько важных нюансов. Так, если речь идет о нише, то размеры углубления прибавляют к полученной цифре, если о выступе – то вычитают.

Также следует отметить, что в жилой комнате часто присутствуют участки, в основе которых лежит окружность. Это может быть как эркерное окно, так и дверной проем в стене, оформленный по типу арки.

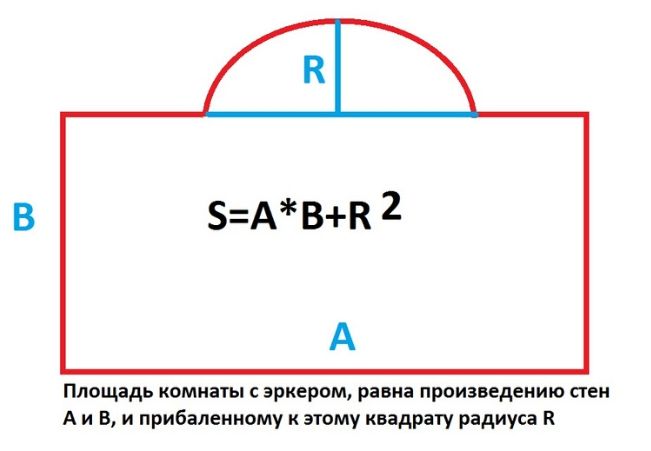
Площадь комнаты с эркером, высчитывается как:

.

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

Схема комнаты с нанесенными измерениями

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

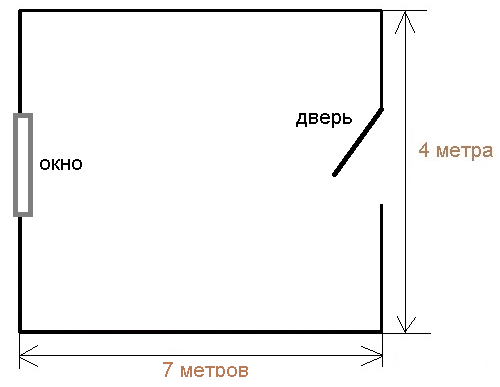
Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

• Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
• Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
• Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

• Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
• Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м².  Снова округлим до 0,67 м².
• Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
• Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

https://youtube.com/watch?v=YL07nZH5ueY

Как посчитать площадь окна

Для многоквартирных многоэтажных домов, а также для типовых проектов индивидуального строительства площадь окна в жилой комнате – параметр, просчитанный специалистами заранее, и для владельца квартиры он не имеет значения, так как уже соответствует всем нормам и стандартам. Но для застройщиков, которые возводят собственное жилье с «нуля», по собственному проекту, площадь окна – такой же важный параметр, как марка цемента или прочность бетона. Расчетная площадь остекления помогает не только сделать правильное освещение в помещении – это и правильная расстановка мебели, и правильные расчеты балки перекрытия проема, и многое другое.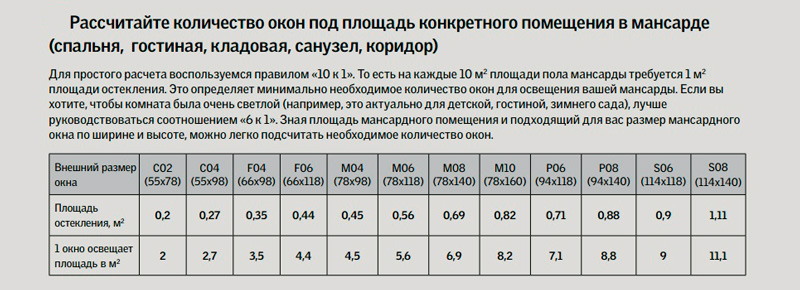

Площадь произвольного треугольника

Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:

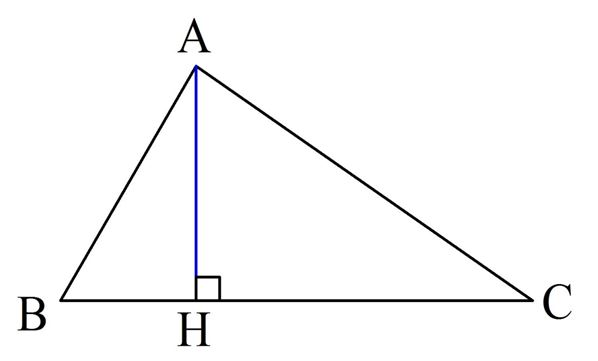
В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:

Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:

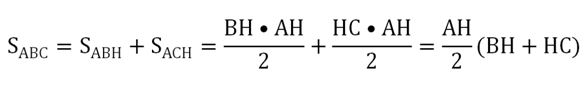
В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:

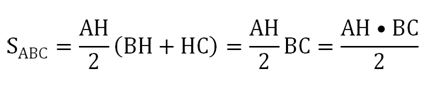
Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):

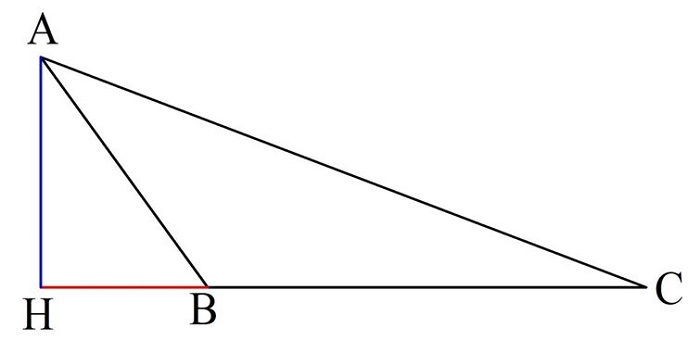
На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:

Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:

Итак, можно сформулировать следующее правило:

Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.

Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.

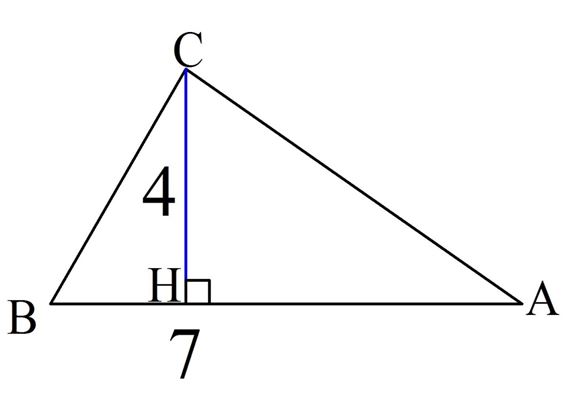
Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:

Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.

Решение.

Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что

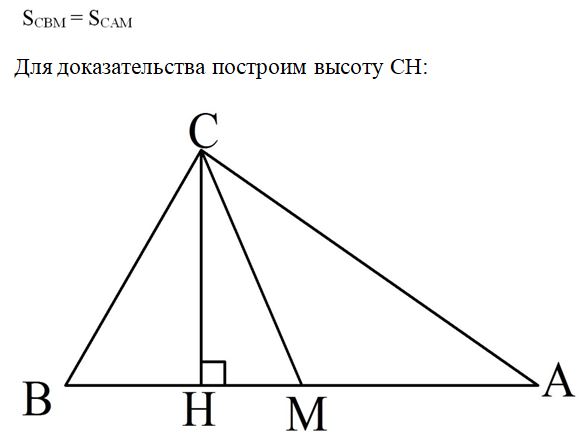
Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а

Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:

Получили одно и то же значение, то есть площади треуг-ков равны.

В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.

Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:

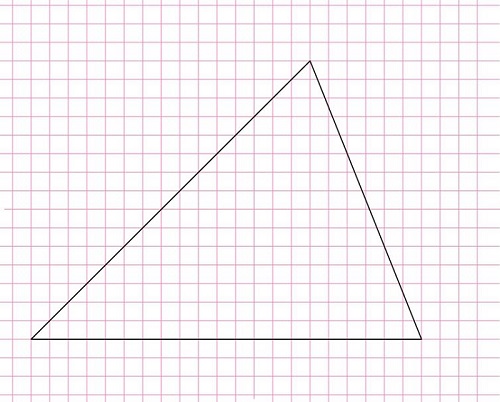
Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:

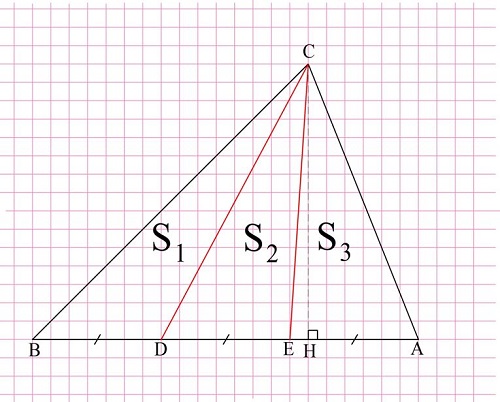
Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:

Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:

Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:

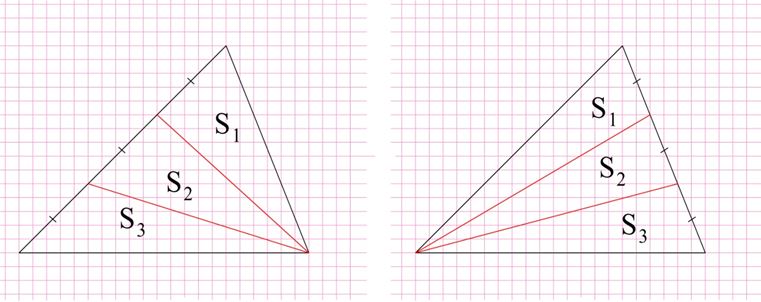
Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.

Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.

Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.

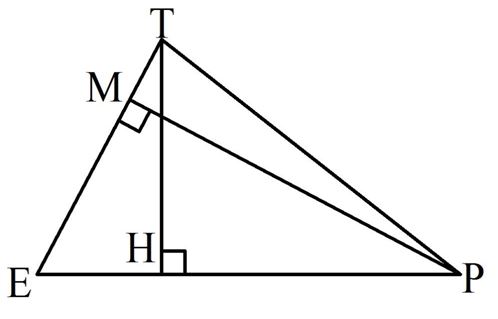
Решение.

Зная ТН и РЕ, мы сможем найти площадь треуг-ка:

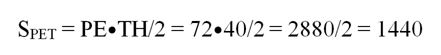
Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ

Величину S_РЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:

Как высчитать квадратуру криволинейного помещения?

Порой в комнатах один из углов «срезан» или стена идёт под углом. Тогда действует тот же принцип деления сложных фигур на более простые, но часть из них будет треугольниками.

В сложных задачах, хороший чертёж – это половина успеха. Составьте план помещения, который поможет «делить» помещение на бумаге, а не в уме.

Скошенные углы в комнате

По сути, такая комната – это прямоугольник, от которого «отрезали» треугольник. Найдя площадь этого треугольника, и вычтя его из общей квадратуры, останется площадь комнаты.

Площадь треугольника находится по формуле:

S = ab:2

Где a и b – это катеты, или стороны перпендикулярные друг другу.

Скошенная же часть – это гипотенуза, которая не требуется для вычислений.

1. Чтобы узнать «a», измеряется ширина той стены, где начинается срез, а затем противоположная стена и находится разница между ними (например, скошенная стена 1,7 м, а противоположная 3 м, значит, «a» = 1,3 м).
2. Аналогично находится «b», только сравниваются длины комнаты (например, 5 м и 3,6 м. Вычисление: 5 – 3,6 = 1,4 м).
3. Вычисляется площадь «срезанного» треугольника (1,3 х 1,4 : 2 = 1,82:2 = 0,91 м2).
4. Согласно сделанным ранее замерам, если бы комнаты была прямоугольной, её габариты были бы 5 м на 3 м. А значит, квадратура 5 х 3 = 15 м2.
5. Из общей квадратуры вычитаем площадь треугольника (15 – 0,91 = 14,09).

Примеры решения

Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:

1. Две стороны.
2. Одна из сторон и диагональ.
3. Диагональ и разность сторон.

Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.

При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.

Геометрия на плоскости

Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед 2 ). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.

Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:

Находится неизвестная сторона: b =(d 2 — a 2 )^(1/2) = (100 — 36)^(1/2) = 8 (м).

Площадь (произведение сторон): S = 6 * 8 = 48 (м 2 ).

Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:

Значение площади будет вычисляться таким образом: S = 2 * ^(1/2) = 2 * 24 = 48 (м 2 ).

Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:

1. Обозначить стороны: a = x и b = x — 3.
2. Составить уравнение: x * (x — 3) = 10.

Раскрыть скобки: x 2 — 3x — 10 = 0.

Нахождение дискриминанта: D = b 2 — 4* a * c = 9 — (4 * 10) 2 ). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.

Источник

Площадь сложных фигур

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

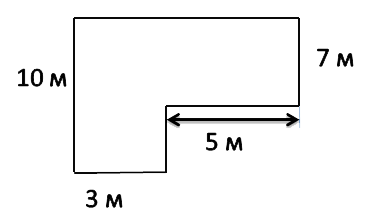
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

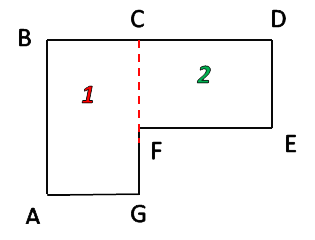_{ABCEEFKLCDEFCDEF}

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников. S = S_ABCE + S_EFKLS = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

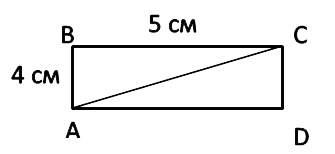
АС — диагональ прямоугольника ABCD . Найдём площадь треугольников

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC S_ABCD = 5 · 4 = 20 см 2

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см 2

S_ABC = S_ACD = 10 см 2

Источник